Thread by Arya AI Dojo 👩🏻💻🤖
- Tweet
- Apr 12, 2023
- #ComputerScience
Thread
All kind of learning is driven by errors!
And how do Neural Networks learn? Let's find out!
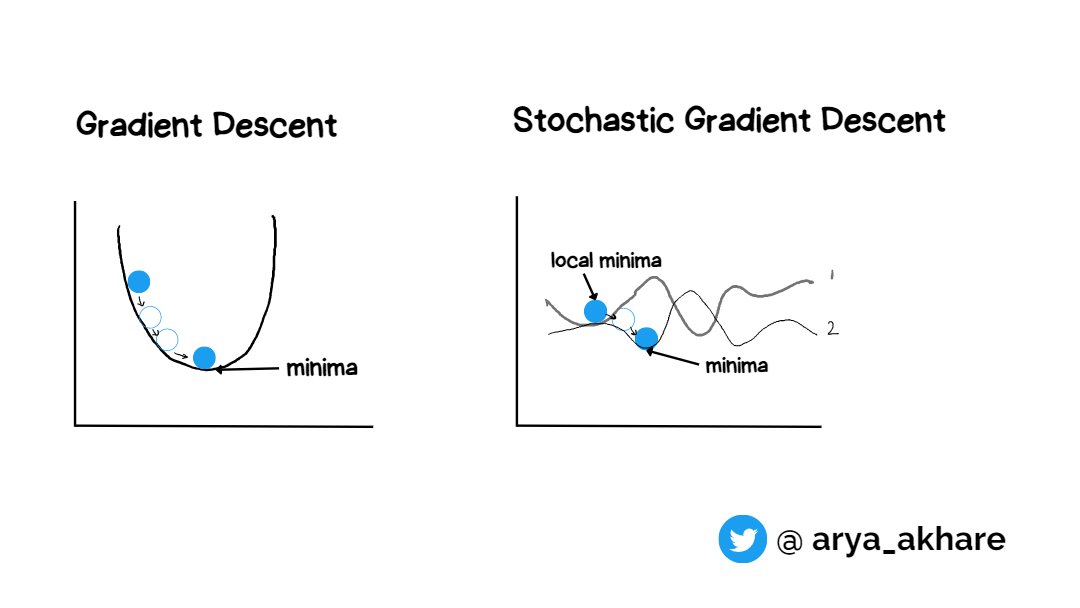
Gradient Descent Algorithm explained with an analogy. A thread🧵
And how do Neural Networks learn? Let's find out!
Gradient Descent Algorithm explained with an analogy. A thread🧵
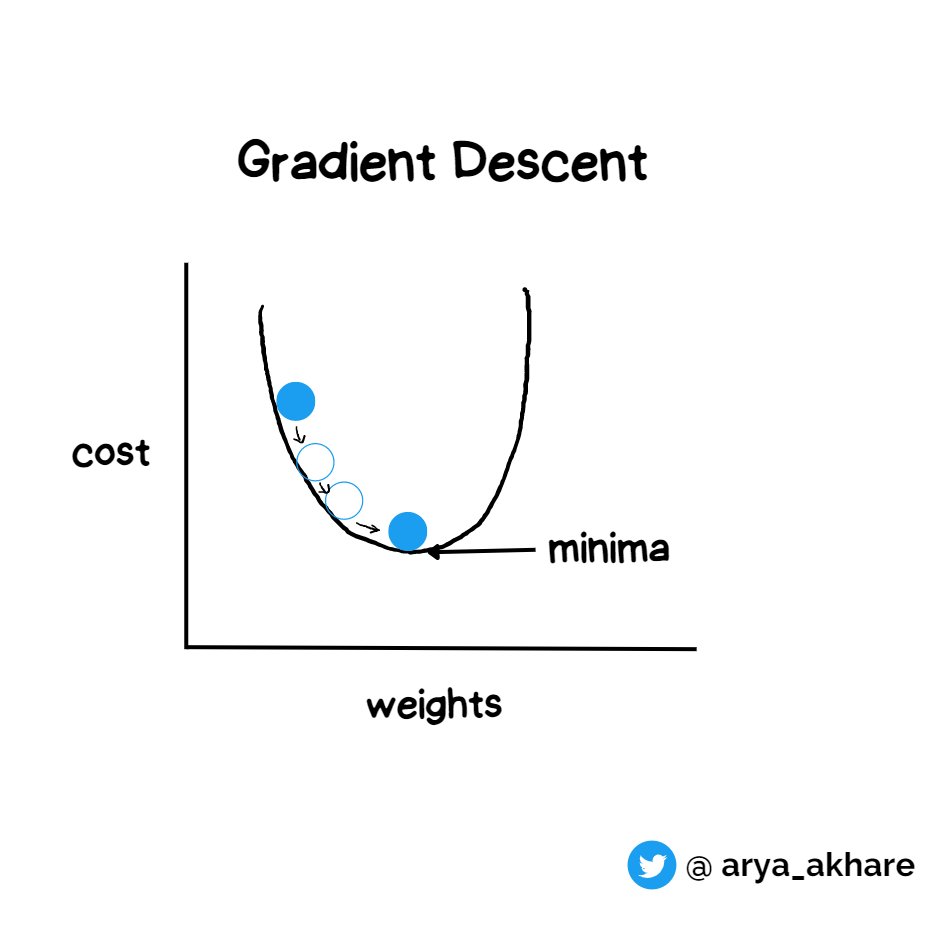
Imagine yourself lost in a mountain valley with one goal in mind, to reach the bottom - this is the basic idea behind Gradient Descent
We have to find such values of weight such that the cost (errors) is minimum.
That lowest point of minimum is known as "minima" (bottom of the valley)
Depending on the type of surface and position, we could be on either a local minima or global minima
That lowest point of minimum is known as "minima" (bottom of the valley)
Depending on the type of surface and position, we could be on either a local minima or global minima
Why do we want minimun error?
Because we want to get our predictions as close to reality (Error= Yreal -Ypredicted)
Because we want to get our predictions as close to reality (Error= Yreal -Ypredicted)
There are three types of the GD Algorithm-
1. Batch Gradient Descent
2. Stochastic Gradient Descent
3. Mini Batch Gradient Descent
1. Batch Gradient Descent
2. Stochastic Gradient Descent
3. Mini Batch Gradient Descent
Analogy-
In Gradient Descent - you are trying to find the lowest point in a valley (the valley representing the cost function)
In Batch Gradient Descent - you are taking large steps in the direction of the steepest slope, using information from all points in the valley
In Gradient Descent - you are trying to find the lowest point in a valley (the valley representing the cost function)
In Batch Gradient Descent - you are taking large steps in the direction of the steepest slope, using information from all points in the valley
In Stochastic Gradient Descent - you are taking small steps using information from only one randomly chosen point in the valley
In Mini-batch Gradient Descent - you are taking medium-sized steps using information from a small randomly chosen group of points in the valley
In Mini-batch Gradient Descent - you are taking medium-sized steps using information from a small randomly chosen group of points in the valley
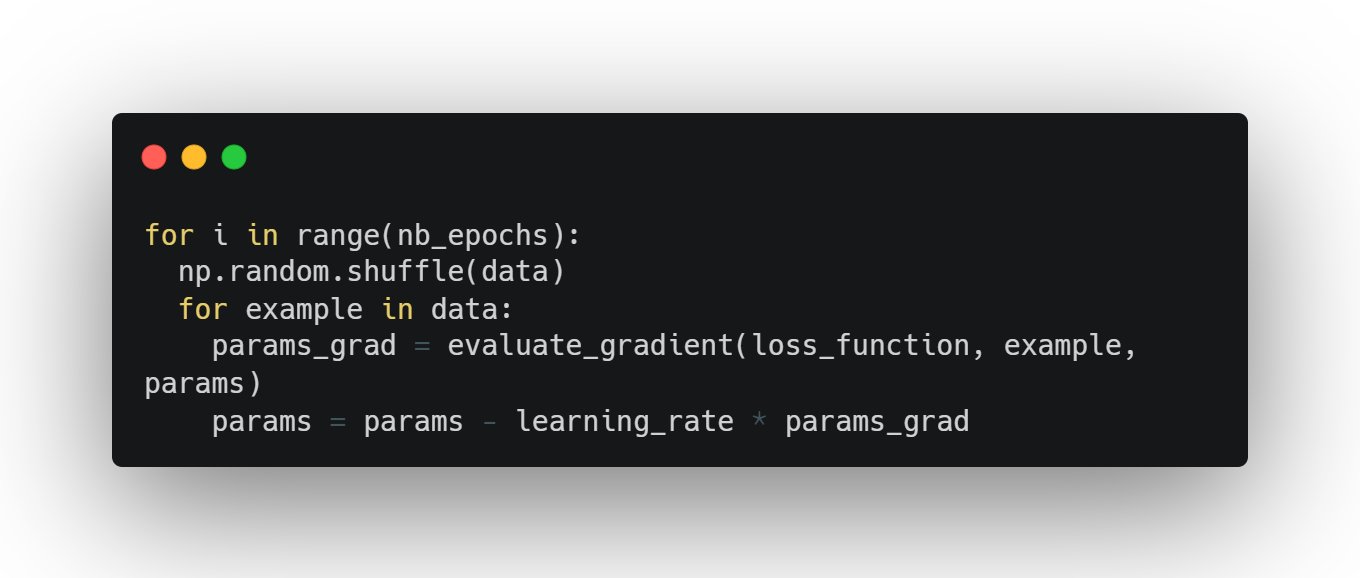
Code and explanation:
1. Batch Gradient Descent
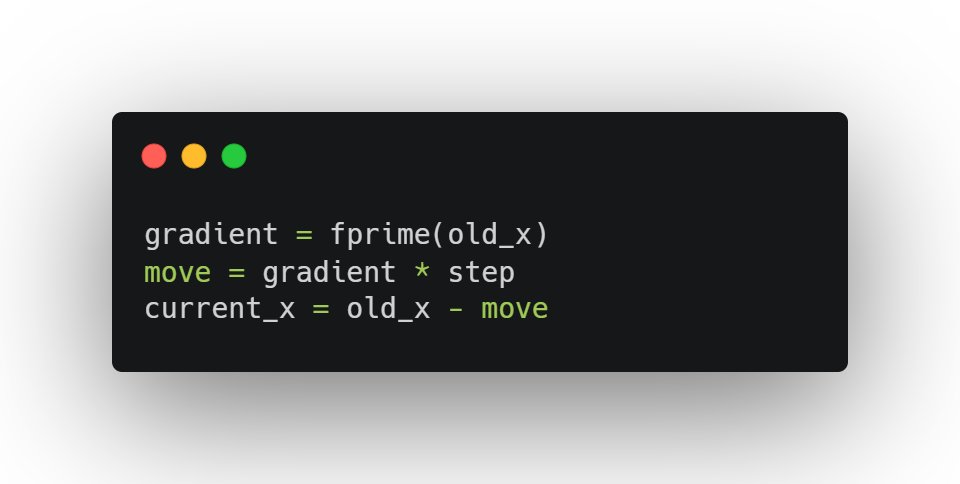
The term gradient means taking the derivative of the function J(x)
J(x) is surface function and its derivative is J'(x) represents the slope at that point
And we use the gradient to move i.e update the value
1. Batch Gradient Descent
The term gradient means taking the derivative of the function J(x)
J(x) is surface function and its derivative is J'(x) represents the slope at that point
And we use the gradient to move i.e update the value
Batch gradient descent is guaranteed to converge to the global minimum for convex error surfaces(bowl-shaped) and to a local minimum for non-convex surfaces
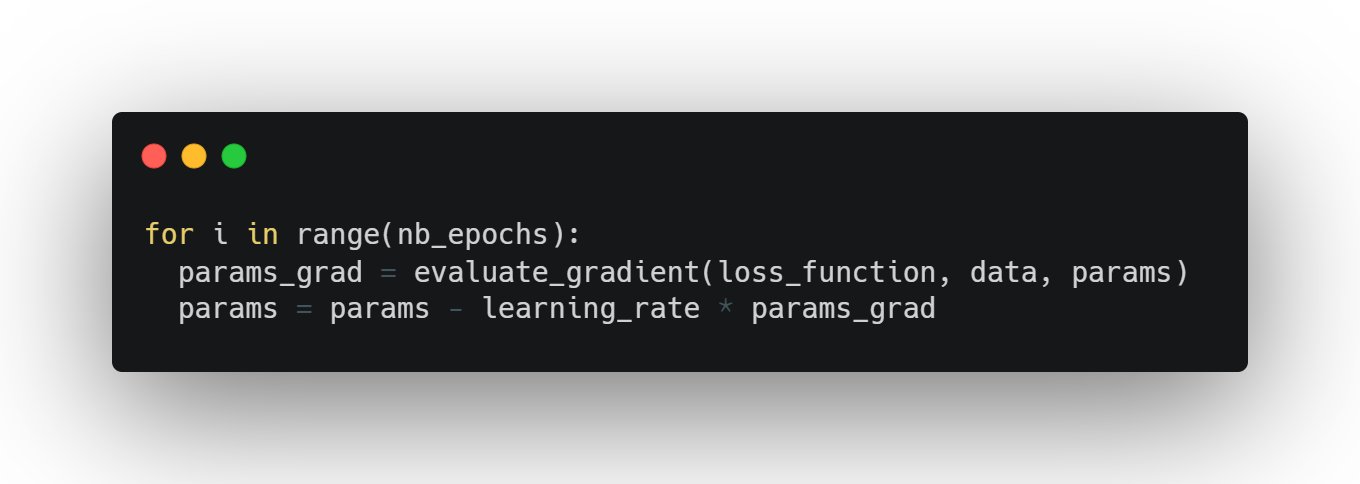
- It uses the entire dataset to calculate errors and update weights
- It is slower to converge but may find the better optima
- It is slower to converge but may find the better optima
2. Stochastic Gradient Descent
The word ‘stochastic‘ means a system or process linked with a random probability.
In this method, at a time only one training example is randomly selected to calculate the gradient and update the parameters at each iteration.
The word ‘stochastic‘ means a system or process linked with a random probability.
In this method, at a time only one training example is randomly selected to calculate the gradient and update the parameters at each iteration.
Due to this, the error surface changes for every data points each having it's own local and global minimas
Imagine dusting your bedsheet, with each movement the surface of the bedsheet is changing in a random manner and the dust bounces off it and falls into another place.
Imagine dusting your bedsheet, with each movement the surface of the bedsheet is changing in a random manner and the dust bounces off it and falls into another place.
We need stochastic gradient descent algorithm to hop off the local minima and fall into another minima
This solves the problem of getting trapped in a local minima using the gradient descent.
This solves the problem of getting trapped in a local minima using the gradient descent.
3. Mini Batch Gradient Descent
It is the same as SGD but here instead of going over all the data points we iterate over them in mini-batches
This approach improves upon the Batch and Stochastic methods by converging faster compared to Batch GD and being more stable than SGD
It is the same as SGD but here instead of going over all the data points we iterate over them in mini-batches
This approach improves upon the Batch and Stochastic methods by converging faster compared to Batch GD and being more stable than SGD
Depending on the complexity of the dataset, balancing right learning rate, the number of iterations required, fitting the right models, and running the optimization for the right time, and the right method is to be used for attaining more accurate solutions in less time.
Thank you so much for reading to the end!
If this thread was helpful to you:
🔁Retweet↗️Share❤️Like
⏩Follow me @arya_akhare and
🤝Connect with me: linkedin.com/in/arya-akhare
for more content around ML/AI like this.
If this thread was helpful to you:
🔁Retweet↗️Share❤️Like
⏩Follow me @arya_akhare and
🤝Connect with me: linkedin.com/in/arya-akhare
for more content around ML/AI like this.
Mentions
See All
Afiz ⚡️ @itsafiz
·
Apr 12, 2023
Great one Arya! Very well explained.