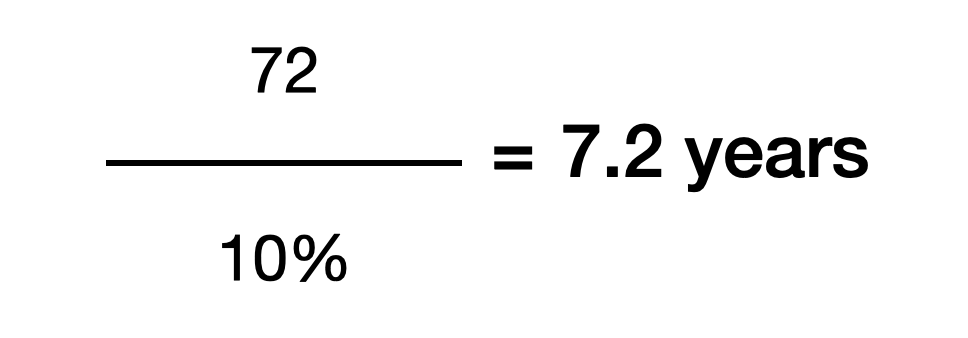Thread
How to calculate when you will double your money on an investment:
1/ The Rule of 72
You can use The Rule of 72 to calculate how many years it will take to double your money on an investment
The one thing you need to know to calculate this is:
The annualized rate of return on your investment
You can use The Rule of 72 to calculate how many years it will take to double your money on an investment
The one thing you need to know to calculate this is:
The annualized rate of return on your investment
Example:
Let’s say you’re looking at an investment that has an annualized return of 10%
How many years will it take to double your money?
You divide 72 by 10% which tells you that you will double your money in over 7 years:
Let’s say you’re looking at an investment that has an annualized return of 10%
How many years will it take to double your money?
You divide 72 by 10% which tells you that you will double your money in over 7 years:
2/ Let’s check the math on this
Let’s say you’ve got $100 to invest and your rate of return is 10% compounded
Here is how much you would have at the end of each year
Year 1: $110
Year 2: $121
Year 3: $133
Year 4: $146
Year 5: $161
Year 6: $177
Year 7: $195
Year 8: $214
Let’s say you’ve got $100 to invest and your rate of return is 10% compounded
Here is how much you would have at the end of each year
Year 1: $110
Year 2: $121
Year 3: $133
Year 4: $146
Year 5: $161
Year 6: $177
Year 7: $195
Year 8: $214
So the Rule of 72 was correct
In just over 7 years, you will double your investment of $100
There are a couple of observations I’d like to draw your attention to in the example above
In just over 7 years, you will double your investment of $100
There are a couple of observations I’d like to draw your attention to in the example above
3/ The rate of return matters
The rule of 72 implies that if you have a higher annual return
You will double your investment quicker
The rule of 72 implies that if you have a higher annual return
You will double your investment quicker
If the annual return in the example above was 20%, you would double your money in just over 3 years:
= 72 / 20% = 3.6 years
At 30%, you would double your money in just over 2 years:
= 72 / 30% = 2.4 years
= 72 / 20% = 3.6 years
At 30%, you would double your money in just over 2 years:
= 72 / 30% = 2.4 years
4/ Compounding accelerates at the end
If you pay close attention to how your investment changes in the example above
You will notice that the gaps start to get bigger at the end
Here is what I mean
If you pay close attention to how your investment changes in the example above
You will notice that the gaps start to get bigger at the end
Here is what I mean
In the later years, your investment increases by + $19
In the early years, your investment increased by +$11
Why is this?
In the early years, your investment increased by +$11
Why is this?
Because the magic of compounding happens at the end
In year 1, earning 10% on $110 is = $11
In year 7, earning 10% on $195 is = $19
In year 1, earning 10% on $110 is = $11
In year 7, earning 10% on $195 is = $19
Because your investment has grown in size over time
In the later years, the same percentage (%) return produces a larger $ number
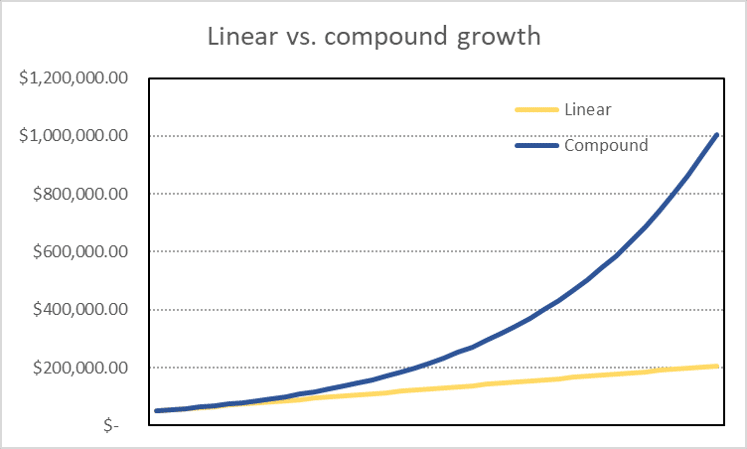
This is why, when you see a graph of compounded growth, it looks like this:
In the later years, the same percentage (%) return produces a larger $ number
This is why, when you see a graph of compounded growth, it looks like this:
5/ Use it in practice
The next time, someone tells you to invest in something
1. Determine what the annual rate of return is
2. Use the rule of 72 to calculate how quickly you will double your money
3. Decide whether or not it’s a good investment for you
The next time, someone tells you to invest in something
1. Determine what the annual rate of return is
2. Use the rule of 72 to calculate how quickly you will double your money
3. Decide whether or not it’s a good investment for you
TL;DR:
1. Figure out: The annual rate of return
2. Use the Rule of 72 to calculate how long it will take to double
3. The higher the rate of return, the quicker it will happen
4. The magic of compounding occurs at the end
1. Figure out: The annual rate of return
2. Use the Rule of 72 to calculate how long it will take to double
3. The higher the rate of return, the quicker it will happen
4. The magic of compounding occurs at the end
Want to improve your understanding of investing and finance?
Sign up for the course I’m creating with @10Kdiver
10kdiver.com/courses/BIBO/
Sign up for the course I’m creating with @10Kdiver
10kdiver.com/courses/BIBO/
@10kdiver If you enjoyed this thread, retweet it so other people can benefit!
Follow @AliTheCFO
I tweet about:
• Finance
• Business Frameworks
• Personal Growth
Follow @AliTheCFO
I tweet about:
• Finance
• Business Frameworks
• Personal Growth
Mentions
See All
Misha @MishadaVinci
·
Jun 12, 2022
Great thread!