Thread
#thermofact
Critical state of gas and liquid
1/ Andrews (1869) reported the experimental discovery. royalsocietypublishing.org/doi/abs/10.1098/rstl.1869.0021
This thread describes experimental observations of critical state, and the thermodynamic theory due to Gibbs (1873).
Critical state of gas and liquid
1/ Andrews (1869) reported the experimental discovery. royalsocietypublishing.org/doi/abs/10.1098/rstl.1869.0021
This thread describes experimental observations of critical state, and the thermodynamic theory due to Gibbs (1873).
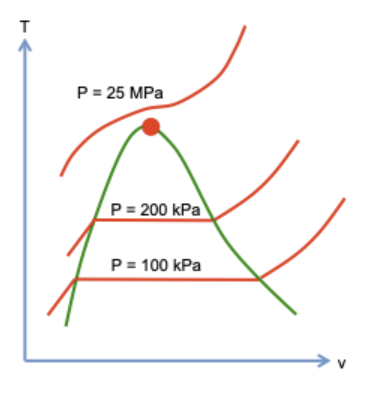
2/ A certain amount of H2O molecules is confined in a cylinder-piston setup. The pressure in the cylinder is held constant, P = 100 kPa.
As temperature changes, the volume changes.
As temperature changes, the volume changes.
3/ Below boiling point Tb, molecules form water, and the volume increases with temperature.
At Tb, the molecules form a mixture of water and steam, and the volume increases as more molecules vaporize.
Above Tb, molecules form steam, and the volume increases with temperature.
At Tb, the molecules form a mixture of water and steam, and the volume increases as more molecules vaporize.
Above Tb, molecules form steam, and the volume increases with temperature.
4/ Repeating the experiment at pressure P = 200 kPa, one obtains another curve on the T-v plane, with a shorter horizontal segment than that for P = 100 kPa.
Repeating the experiment at P = 25 MPa, one does not observe horizontal segment.
Repeating the experiment at P = 25 MPa, one does not observe horizontal segment.
5/ Repeating the experiments for many pressures, one obtains many curves on the T-v plane.
As the pressure increases, the horizontal segment becomes shorter. At a critical pressure, the segment becomes a point, called the critical state.
Pc = 22 MPa
Tc = 374 C
vc = 0.003 m3/kg
As the pressure increases, the horizontal segment becomes shorter. At a critical pressure, the segment becomes a point, called the critical state.
Pc = 22 MPa
Tc = 374 C
vc = 0.003 m3/kg
6/ One can also do experiment at a constant temperature, and measure pressure as a function of volume.
7/ Boiling temperature increases with pressure. But the curve terminates at the critical state, beyond which no phase change is observed.
8/ Experiments like these over the years have been summarized in the form of Steam Tables.
Data are available for many types of molecules, not just H2O molecules.
#thermofact
Data are available for many types of molecules, not just H2O molecules.
#thermofact
9/ I next describe the theory of critical state due to Gibbs (1873).
His theory entered classic textbooks by Maxwell and Planck, but has been purged from later textbooks.
I will use today's language.
drive.google.com/file/d/1EoKZ9mE3SHUJhQo9RlSFfQUDX__gcfVK/view?usp=sharing
His theory entered classic textbooks by Maxwell and Planck, but has been purged from later textbooks.
I will use today's language.
drive.google.com/file/d/1EoKZ9mE3SHUJhQo9RlSFfQUDX__gcfVK/view?usp=sharing
10/ Thermodynamics of a system of a species of molecules has two independent variables: energy and volume.
When energy and volume are fixed, the system becomes an isolated system, flipping among a set of quantum states.
Entropy is the logarithm of the number of quantum states.
When energy and volume are fixed, the system becomes an isolated system, flipping among a set of quantum states.
Entropy is the logarithm of the number of quantum states.
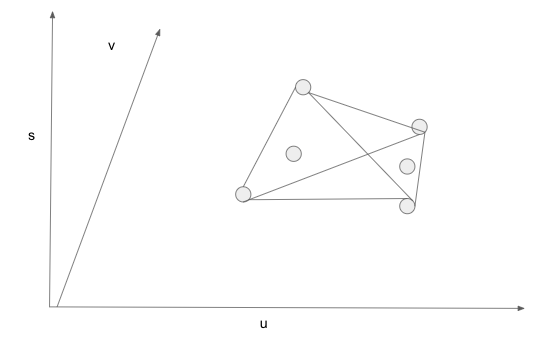
11/ Let u, v, s be average energy, volume, entropy per molecule.
Draw a three-dimensional space, spanning u and v as the horizontal plane, and erecting s as the vertical axis.
A homogeneous state of the system is a point in the space.
I mark some homogeneous states.
Draw a three-dimensional space, spanning u and v as the horizontal plane, and erecting s as the vertical axis.
A homogeneous state of the system is a point in the space.
I mark some homogeneous states.
12/ Energy, volume, entropy are extensive properties. A mixture of two or more homogeneous states is a linear combination of these homogenous states.
Given a set of homogeneous states, all mixtures form the convex hull of these homogeneous states.
Given a set of homogeneous states, all mixtures form the convex hull of these homogeneous states.
13/ For a set of discrete points in a three dimensional space, the convex hull consists of triangles. Each triangle connects three points.
en.wikipedia.org/wiki/Convex_hull
en.wikipedia.org/wiki/Convex_hull
14/ The system is an isolated system when energy and volume are fixed, corresponding to a vertical line.
The isolated system equilibrates by maximizing entropy, corresponding to the point of interaction between the vertical line and the upper boundary of the convex hull.
The isolated system equilibrates by maximizing entropy, corresponding to the point of interaction between the vertical line and the upper boundary of the convex hull.
15/ As energy and volume vary, the vertical line move, and the entire upper boundary of the convex hull constitute all equilibrium states.
An equilibrium state can be a homogeneous state, a mixture of two homogeneous states, or a mixture of three homogeneous states.
An equilibrium state can be a homogeneous state, a mixture of two homogeneous states, or a mixture of three homogeneous states.
16/ Gibbs assumed that homogeneous states of gas and homogeneous states of liquid form a single surface in the (s,u,v) space.
He further assumed that the surface is non-convex.
The convex hull is constructed by rolling a tangent plane over the surface.
He further assumed that the surface is non-convex.
The convex hull is constructed by rolling a tangent plane over the surface.
17/ The system of molecules has two independent thermodynamic properties, u and v. Every other thermodynamic property is a function of u and v.
In particular, consider the function s(u,v) for all homogeneous states. This function corresponds to the non-convex surface.
In particular, consider the function s(u,v) for all homogeneous states. This function corresponds to the non-convex surface.
18/ Gibbs further assumed that the function s(u,v) for homogeneous states is smooth, having partial derivatives with respect to u and v.
Recall the identity
ds = (1/T)du + (P/T)dv.
Thus, 1/T and P/T are the two partial derivatives, corresponding to slops of tangent plane.
Recall the identity
ds = (1/T)du + (P/T)dv.
Thus, 1/T and P/T are the two partial derivatives, corresponding to slops of tangent plane.
19/ Homogenous states define a smooth, non-convex surface s(u,v).
Equilibrium states define the upper boundary of the convex hull, which is formed by rolling a tangent plane over the smooth, non-convex surface.
The two slopes of the tangent plane are 1/T and P/T.
Equilibrium states define the upper boundary of the convex hull, which is formed by rolling a tangent plane over the smooth, non-convex surface.
The two slopes of the tangent plane are 1/T and P/T.
20/ When the tangent plane touches the non-convex surface at one point, this point belongs to the upper boundary of the convex hull.
Such a point corresponds to a homogeneous state of equilibrium, either a state of water, or a state of steam.
Such a point corresponds to a homogeneous state of equilibrium, either a state of water, or a state of steam.
21/ When the tangent plane touches the non-convex surface at two points, the line segment connecting the two points belongs to the upper boundary of the convex hull.
The ends of the segment represent two homogeneous states, which have an equal temperature and an equal pressure.
The ends of the segment represent two homogeneous states, which have an equal temperature and an equal pressure.
22/ A point on the segment represents an equilibrium mixture of the two homogeneous states.
Rolling the tangent plane on the surface forms a new surface, which belongs to the upper boundary of the convex hull.
The new surface meets the non-convex surface at two curves.
Rolling the tangent plane on the surface forms a new surface, which belongs to the upper boundary of the convex hull.
The new surface meets the non-convex surface at two curves.
23/ The two curves meet at a point, which represents the critical state.
The Gibbs theory interprets various experimental observations by representing all homogeneous states with a smooth, non-convex surface s(u,v).
The theory does not give the molecular origin of the surface.
The Gibbs theory interprets various experimental observations by representing all homogeneous states with a smooth, non-convex surface s(u,v).
The theory does not give the molecular origin of the surface.
24/ This thread on critical state is adapted from my class notes on thermodynamics.
I write this thread so that people can critique point by point.
docs.google.com/document/d/12j5d-QBfZGoF-31RLIpK0gY6HAcvMe-yc4FnkRh06kg/edit
I write this thread so that people can critique point by point.
docs.google.com/document/d/12j5d-QBfZGoF-31RLIpK0gY6HAcvMe-yc4FnkRh06kg/edit
25/ Wordings in some of the tweets above should be made precise.
All mixtures are represented by the convex hull of given homogeneous states.
The convex hull is a solid figure in the (u,v,s) space.
The upper boundary of the convex hull represents all equilibrium states.
All mixtures are represented by the convex hull of given homogeneous states.
The convex hull is a solid figure in the (u,v,s) space.
The upper boundary of the convex hull represents all equilibrium states.
26/ The Wikipedia entry on "convex hull" lists several applications. I just add one: thermodynamics, with a reference: this thread.😀
Let's see how others edit.
@TheAzizLab @martinmbauer @matloff @Cyberplasm @stevenstrogatz @gravity_levity @ProfZhaoMIT
en.wikipedia.org/wiki/Convex_hull
Let's see how others edit.
@TheAzizLab @martinmbauer @matloff @Cyberplasm @stevenstrogatz @gravity_levity @ProfZhaoMIT
en.wikipedia.org/wiki/Convex_hull
27/ I also modify the general introduction of the Wikipedia entry a little to change "Euclidean space" to "real vector space".
I do so to accommodate the following fact:
The energy-volume-entropy space is a real vector space with no inner product. It is not a Euclidean space.
I do so to accommodate the following fact:
The energy-volume-entropy space is a real vector space with no inner product. It is not a Euclidean space.
28/ Yesterday a Wikipedia Editor reverted my additions to the entry "Convex hull" for two reasons.
1. Tweets are not considered to be reliable sources on Wikipedia.
2. I should not cite my own tweets.
I've modified the additions, which cite Gibbs (1873).
I took a screenshot⬇️
1. Tweets are not considered to be reliable sources on Wikipedia.
2. I should not cite my own tweets.
I've modified the additions, which cite Gibbs (1873).
I took a screenshot⬇️
29/ My updated additions have just been reverted again by a different Wikipedia Editor. This time, no reason is given.
30/ Upon a closer reading, I found an explanation from the reverter:
"Translating old papers in today's language is WP:OR."
I clicked WP:OR, and landed on this page⬇️
en.wikipedia.org/wiki/Wikipedia:No_original_research
"Translating old papers in today's language is WP:OR."
I clicked WP:OR, and landed on this page⬇️
en.wikipedia.org/wiki/Wikipedia:No_original_research
31/ The Wikipedia provides an "undo" button. I clicked the button and restored my additions. I provided the following explanation.
en.wikipedia.org/wiki/Convex_hull
en.wikipedia.org/wiki/Convex_hull
32/ On further reflection, one sees that Gibbs (1873) survives the purge and lives in a different form.
True, energy-volume-entropy space is purged from textbooks.
But the plane of composition and free energy is used, where mixtures form the convex hull of homogenous states.
True, energy-volume-entropy space is purged from textbooks.
But the plane of composition and free energy is used, where mixtures form the convex hull of homogenous states.
33/ My additions were reverted for the third time! A new reason was given:
"And even if it had a source, it is presented far out of proportion to its significance."
Really?
The Gibbs method is used to analyze thermodynamic phases.
I modified and added again.
Screenshot⬇️
"And even if it had a source, it is presented far out of proportion to its significance."
Really?
The Gibbs method is used to analyze thermodynamic phases.
I modified and added again.
Screenshot⬇️
34/ My little additions to Wikipedia on a convex hull in thermodynamics have survived for more than two days.😅
Please take a look, revise, and comment.
en.wikipedia.org/wiki/Convex_hull
Please take a look, revise, and comment.
en.wikipedia.org/wiki/Convex_hull