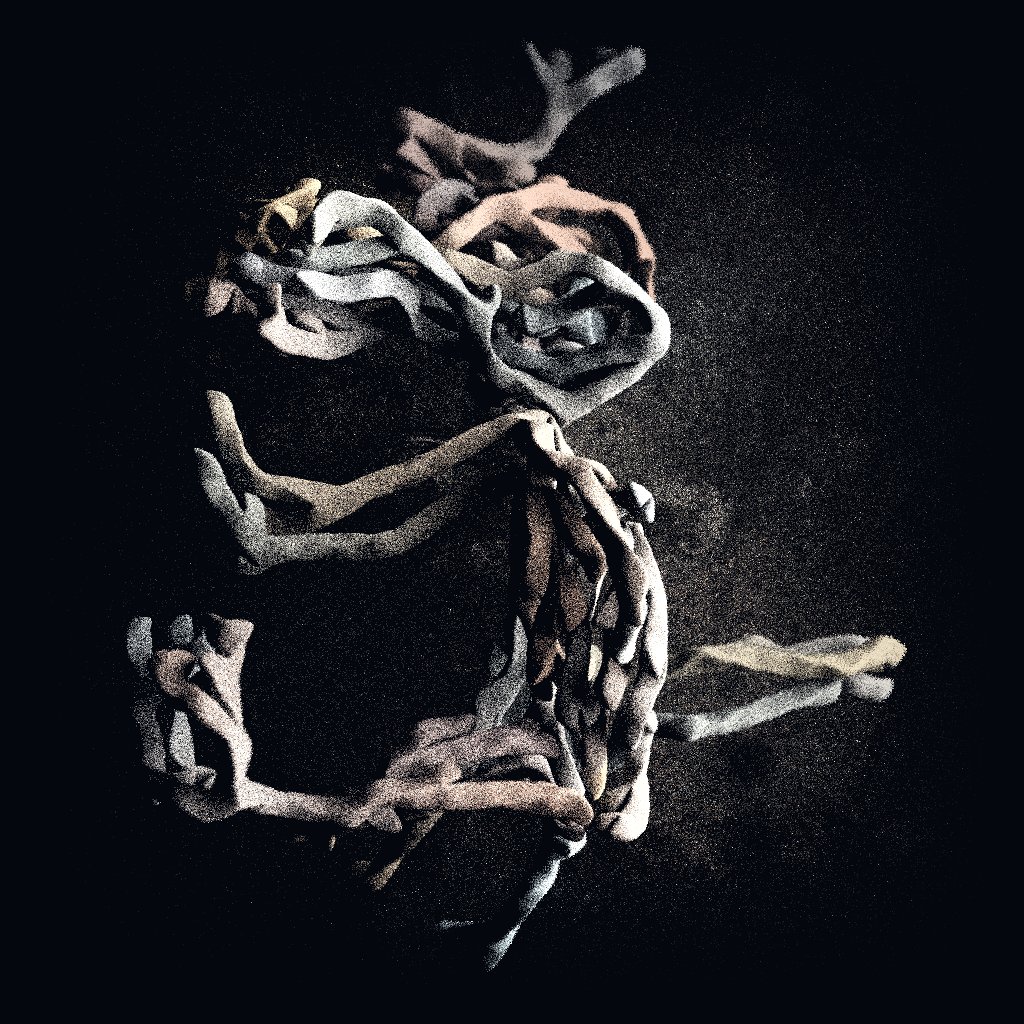Thread by (rat)chitect - Alejandro
- Tweet
- Jan 17, 2023
- #DigitalArt
Thread
Today, I minted this beautiful iteration of 7.356
Why is @jMarkusiewicz's 7.356 degrees amazing?
A short thread of appreciation
🧵👇 1/7
Why is @jMarkusiewicz's 7.356 degrees amazing?
A short thread of appreciation
🧵👇 1/7
2/7 As you probably know, I'm a real Jacek fan. Though he has a much more dark (😉) style than what I usually do, I find his work full of care and meanings. He is a real digital craftsman that puts lots of thought on every piece he makes.
Simply look at this loading screen!
Simply look at this loading screen!
3/7 Let's take a look at the idea behind 7.356:
"When you connect five pyramids by attaching their faces, you will be left with a thin empty space: a volumetric angle of 7.356 degrees. It’s too small to fit another piece and too big to be lost in numerical imprecision."
"When you connect five pyramids by attaching their faces, you will be left with a thin empty space: a volumetric angle of 7.356 degrees. It’s too small to fit another piece and too big to be lost in numerical imprecision."
4/7
"It is a surprising imperfection. [...] you cannot use your building block to fully fill a void. It’s as if the mathematical rules –the ones we tend to idealise for elegance, harmony, and infallibility– broke when you raise complexity."
owned by @ajberni
"It is a surprising imperfection. [...] you cannot use your building block to fully fill a void. It’s as if the mathematical rules –the ones we tend to idealise for elegance, harmony, and infallibility– broke when you raise complexity."
owned by @ajberni
5/7
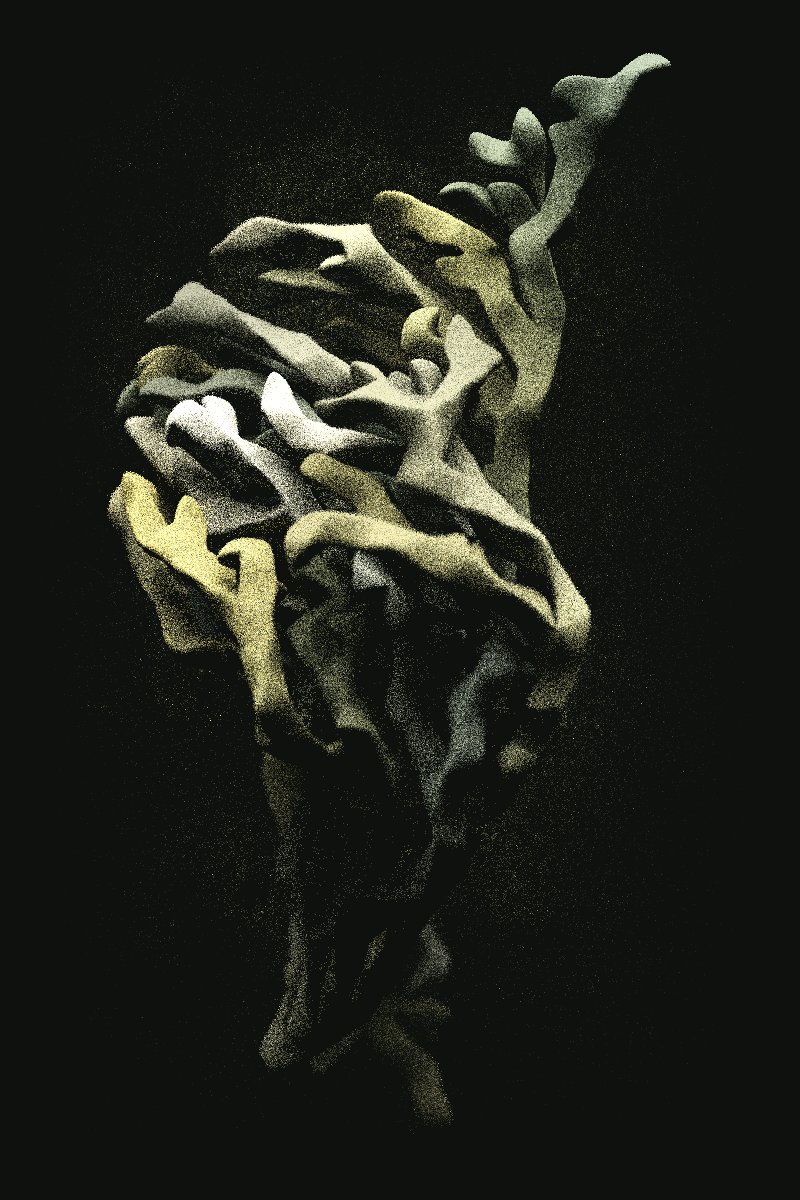
"But mathematical beauty does not reside in perfection. [...] So keep building [...] and embrace the surprising, chaotic aesthetics that appears. A different type of harmony – not based on impeccable proportions, but on unpredictability."
owned by @williamapan
"But mathematical beauty does not reside in perfection. [...] So keep building [...] and embrace the surprising, chaotic aesthetics that appears. A different type of harmony – not based on impeccable proportions, but on unpredictability."
owned by @williamapan
6/7 There could be a case whether something fits or does not fit one's taste. But Art is not about taste.
7.356 is the beauty of imperfection, of an artist pursuing something meaningful until its latest unpredictable consequences.
owned by @lemonde2d
7.356 is the beauty of imperfection, of an artist pursuing something meaningful until its latest unpredictable consequences.
owned by @lemonde2d
7/7
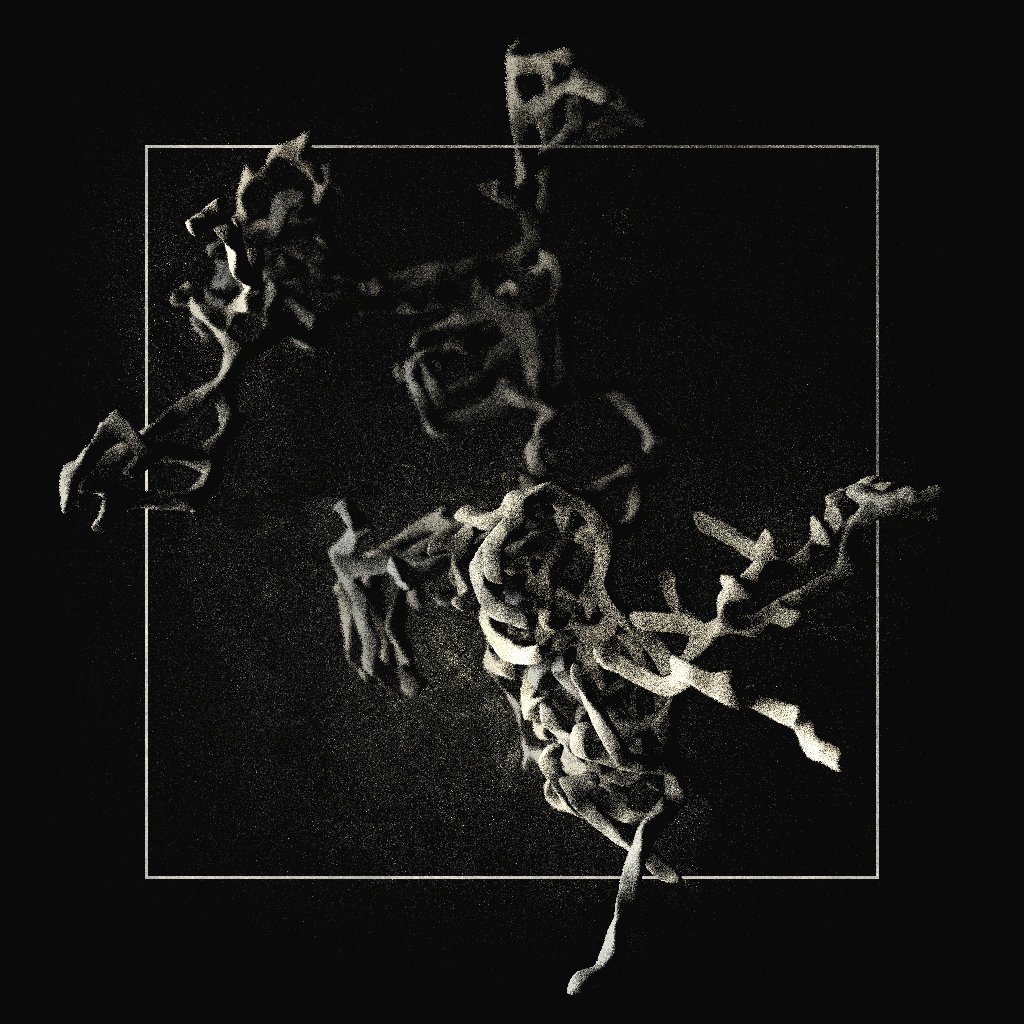
This project reflects Jacek's worldview, his genealogy, and his artistic journey.
Jacek is an artist. He's living in a digital era, and uses the generative tools to perfection. But, if he had been born in 1600, he would use stone to carve his 7.356 degrees.
owned by @seth
This project reflects Jacek's worldview, his genealogy, and his artistic journey.
Jacek is an artist. He's living in a digital era, and uses the generative tools to perfection. But, if he had been born in 1600, he would use stone to carve his 7.356 degrees.
owned by @seth
CODA.
One can easily evaluate the quality of a collection by its collectors. I've picked here the pieces bought by some of the most intelligent Tezos artists/collectors.
Do not follow my advice. This is not an investment, but a token of support.
(owned by @jMarkusiewicz)
One can easily evaluate the quality of a collection by its collectors. I've picked here the pieces bought by some of the most intelligent Tezos artists/collectors.
Do not follow my advice. This is not an investment, but a token of support.
(owned by @jMarkusiewicz)
And DISCLAIMER
I minted one of these, but haven't bought on secondary, and not planning to buy. I tend to collect one of each by Jacek, with no plans of selling.
I minted one of these, but haven't bought on secondary, and not planning to buy. I tend to collect one of each by Jacek, with no plans of selling.
And CODA2
The most difficult part of a long-form generative collection is guaranteeing a consistent quality of the outputs. This is an extreme example of a collection that, simply, doesn't have bad outputs.
So perfect for an algorithm craving on imperfection!
The most difficult part of a long-form generative collection is guaranteeing a consistent quality of the outputs. This is an extreme example of a collection that, simply, doesn't have bad outputs.
So perfect for an algorithm craving on imperfection!