Thread
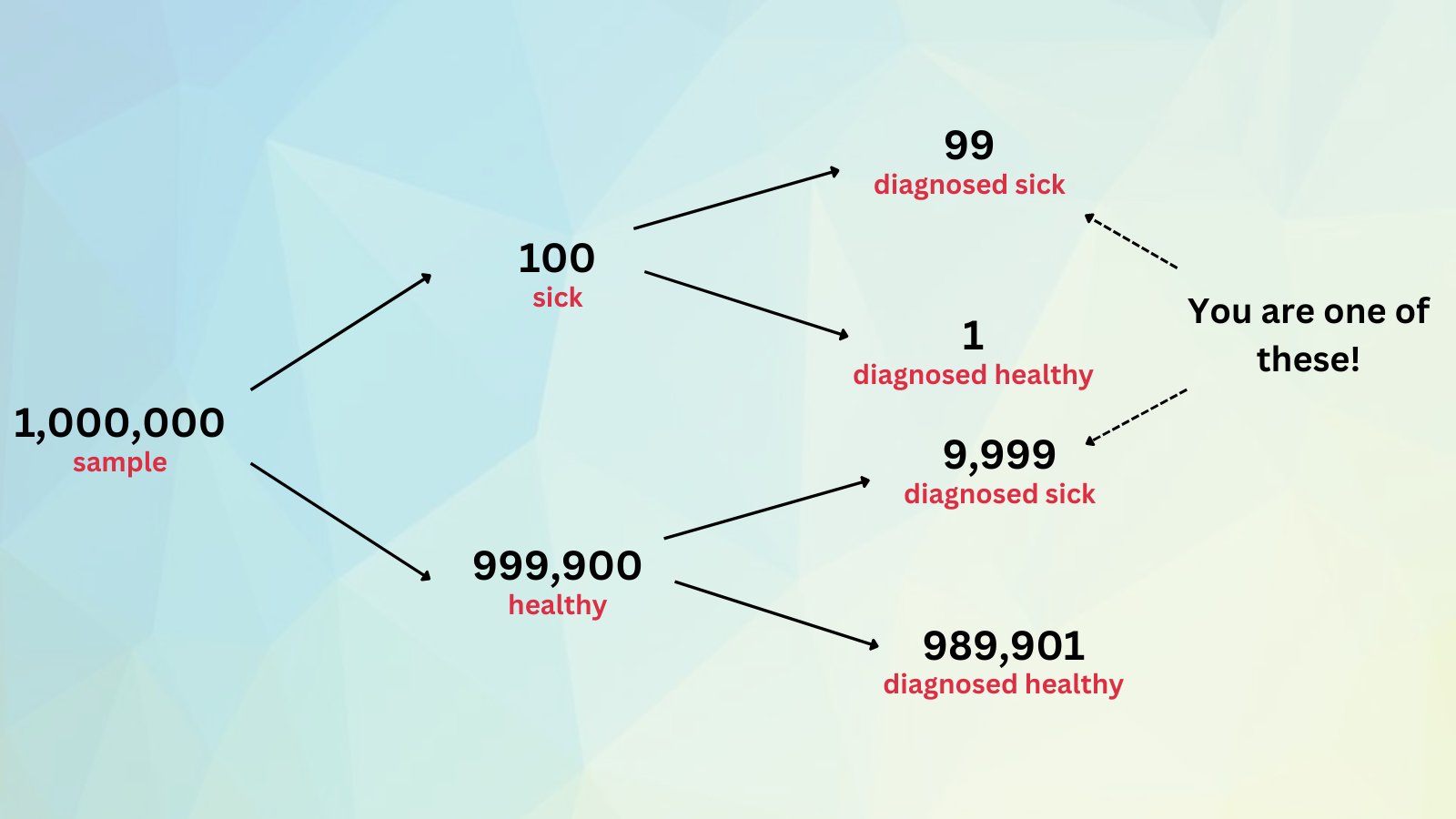
In this 🧵 We will calculate with the numbers from the disease example.
You can find the example here:
1/8
You can find the example here:
1/8
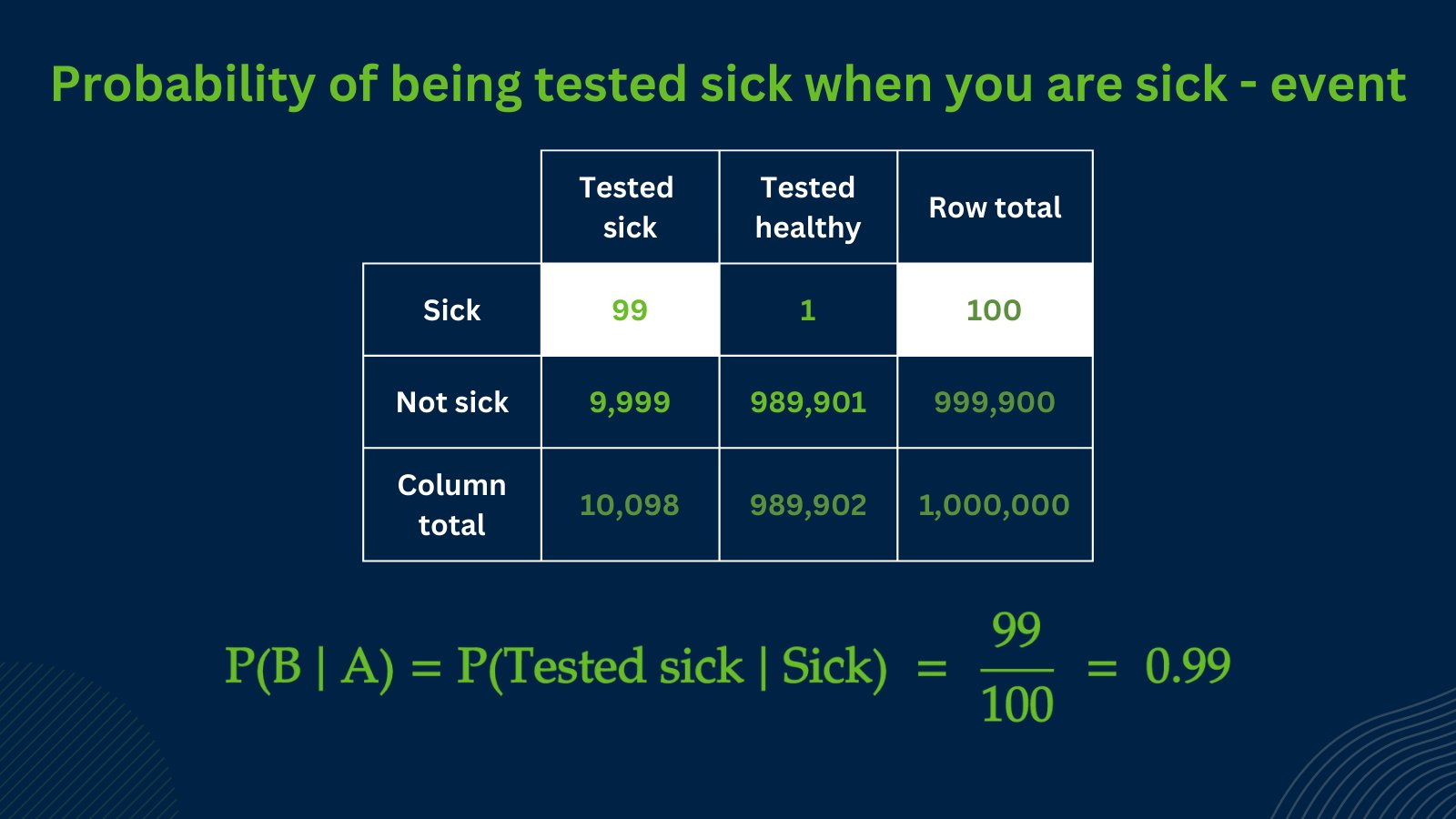
We want to know:
What is the probability that you have the disease given that you have tested positive?
Mathematically,
P(A | B) = P(You have disease | Tested positive)
So
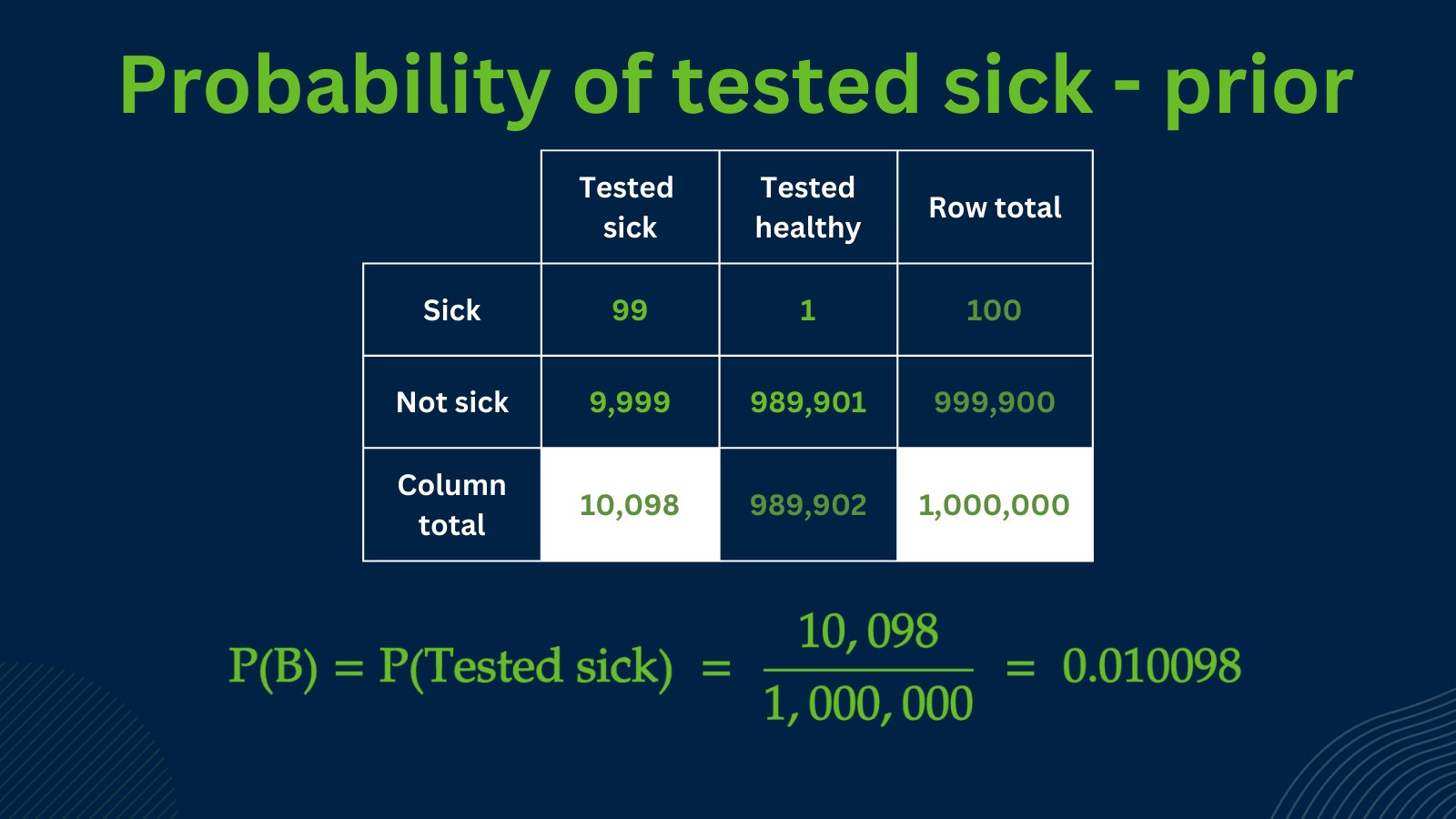
A = sick
B = tested positive
3/8
What is the probability that you have the disease given that you have tested positive?
Mathematically,
P(A | B) = P(You have disease | Tested positive)
So
A = sick
B = tested positive
3/8
Now let's do the math.
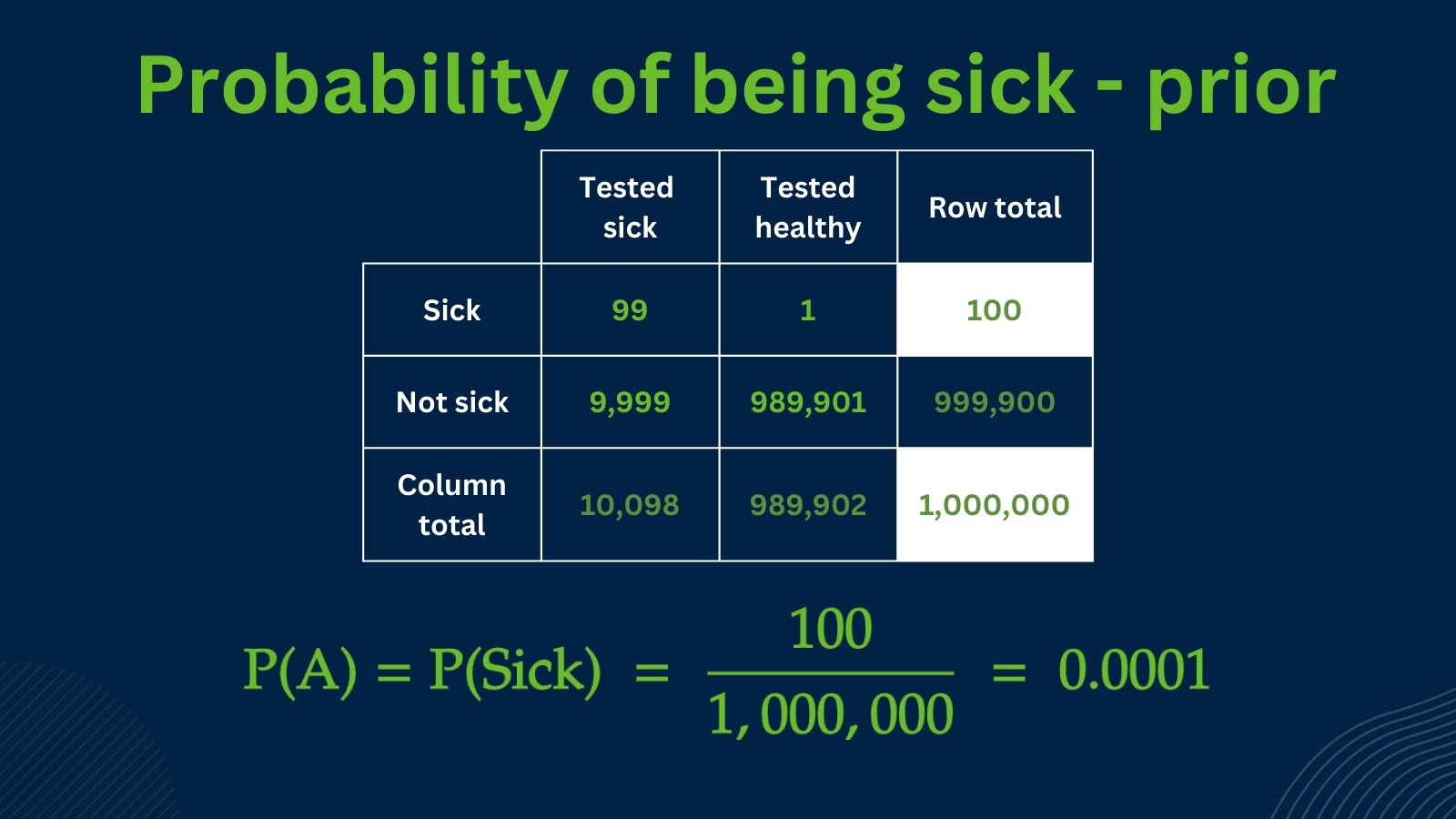
1. Calculate P(A) namely the probability of being sick, this is our first prior.
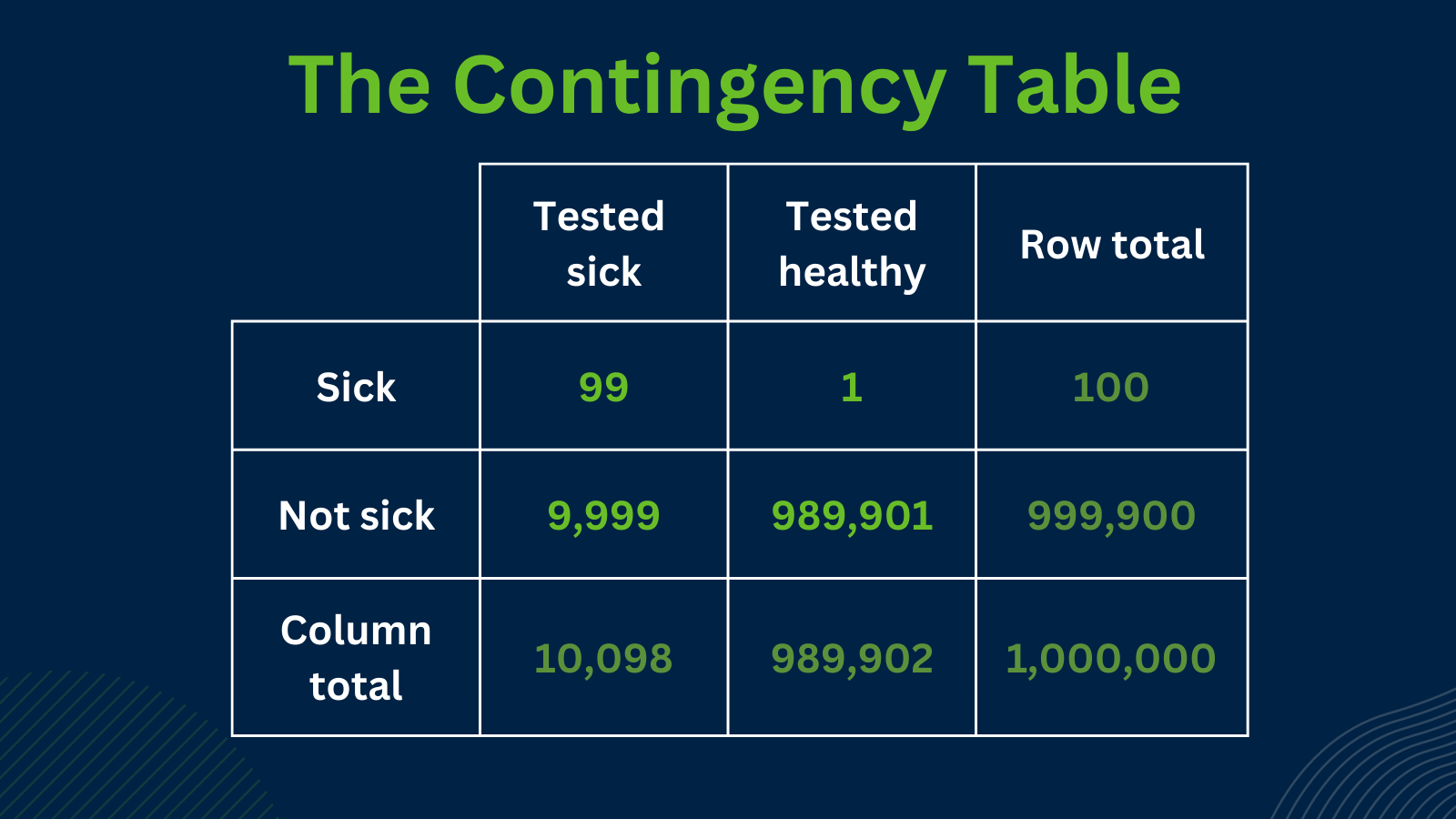
Note: we can calculate this from the table, or from the given information:
We know that 1 out of every 10,000 patients is sick.
4/8
1. Calculate P(A) namely the probability of being sick, this is our first prior.
Note: we can calculate this from the table, or from the given information:
We know that 1 out of every 10,000 patients is sick.
4/8
Now we can put everything together 🔽
The probability of being sick when you are tested sick is less than 1%.
7/8
The probability of being sick when you are tested sick is less than 1%.
7/8
That's it for today.
I hope you've found this thread helpful.
Like/Retweet the first tweet below for support and follow @levikul09 for more Data Science threads.
Thanks
8/8
I hope you've found this thread helpful.
Like/Retweet the first tweet below for support and follow @levikul09 for more Data Science threads.
Thanks
8/8
Mentions
See All
Jaydeep Karale @_jaydeepkarale
·
Mar 12, 2023
Great one, Levi